John Hopfield just received a Nobel prize, so I thought about implementing his network from the 80s. A Hopfield network is a type of Recurrent Network which was actually discovered even before Rumelhard’s first RNN. It contains a single layer of neurons and each neuron is connected to every other neuron except itself (fully connected network). The connections are bidirectional and symmetric, so wij = wji.
During training, we update the weights using the Hebbian rule and the state of neurons using the energy function minimization.
I. The Hebbian rule
The Hebbian rule means that neurons which fire together, wire together, and this is best represented mathematically as an outer product between all neurons. The connection between 2 neurons should be strengthened if they are both active at the same time. So, by doing the outer product with itself, where each neuron is multiplied with all the other ones, we get this fully connected representation. We can visualise this matrix created as memories being embeded in the brain.
In our case, let’s suppose we are learning a series of 3 patterns X = [x1,x2,x3]. In this case, we loop through each pattern and we do an outer product of each pattern with itself. Then, we do an avearge, by summing the result and divide it by the number of patterns:
1
2
3
4
for x in X: # x is a pattern
weights += np.outer(x, x) / m # outer product with itself.
weights[np.diag_indices(n_units)] = 0 # we want the diagonal to be 0 because the neurons don't have connections between themselves
The formula for the hebbing rule which was implemented above is:
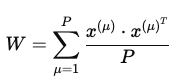where:
- P = the number of patterns.
- W = the weight matrix
- μ = one pattern
- x = the neurons from one pattern
Once these weights are learned, they remain fixed. They encode the patterns as attractor states in the energy landscape of the network. We can view the weight matrix resulted as the energy landscape where each pattern will act like local minima. This was the act of learning the energy landscape.
This weights matrix will have a shape equal to the number of neurons, both vertical and horizontal. In case of images we will use each neuron to correspond with a pixel, so a 26 pixel image (pattern) will be represented by a matrix of size 26x26.
II. Energy minimization
The neuron states x represent the current activity of the networks and they will evolve during the process of recall of a pattern. We call this step, the act of inference, where we are recalling the memory of the pattern. We received the network with the weights learned, now we need to find which neurons are active and which aren’t for a specific pattern. Remember that the weights will remain fixed during this process.
We start from an incomplete (noisy) pattern and we want to recall the true pattern. We do this by taking all the neurons one at a time and update it. The state of the neuron i will be:
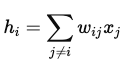
where:
- wij is the weight of the connection between neuron i and neuron j.
- xj is the current state of neuron j (-1 or +1).
- j != i because neurons don’t have connections with themselves
So hi will be computed as an inner product between the weights and all other neurons:
hi = wi1x1 + wi2x2 + … + wiNxN
After we compute hi, we update the state of the neuron xi using the following activation function:
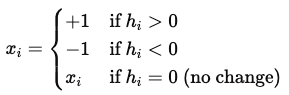
Here, 0 is our threshold. We can also opt for a hyperbolic tangent function xi = tanh(hi) to make the updates smoother. This soft activation allows the state of the neuron to take continuous values between -1 and +1. So, if the sum of all connections with other neurons and their weights is positive of xi, then we make xi positive, otherwise, we make it negative. This way, it is guaranteed that the energy is minimized step by step.
Here is how we would do it in python:
1
2
3
4
5
6
7
8
n_iter = 10 # 10 iterations of training
Xs = [None] * n_iter # This list will store the state of X after each iteration.
for i in range(n_iter):
X = np.dot(X, weights) # X (the current pattern) is multiplied by the weight matrix (inner product).
X[X < 0] = -1 # Neurons with negative inputs are set to −1
X[X >= 0] = 1 # Neurons with non-negative inputs are set to +1
Xs[i] = X # Saves the current state of X in the ith slot of Xs. This allows tracking how X evolves over iterations.
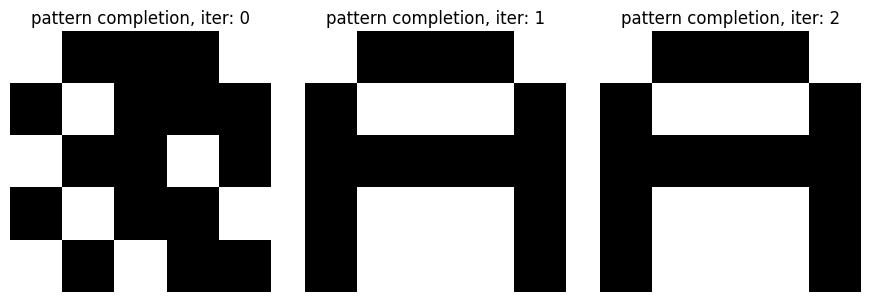
We start with the weights matrix built previously, which is our landscape, and we know have to descend in this landscape to find the local minima for each pattern that we want to recover. We will start with a corrupted pattern, X, which we want to recall. During 10 iterations we will update this X by doing an inner product with the weight matrix.
X will have a shape of 26 and weights has a shape of (26,26), and the result of a dot product between them is of shape 26. Then we set the neurons with negative inputs to -1 and the other ones to +1. This way, the network will evolve toward a state with lower energy, which corresponds to the stored patterns. This update guarantees that the consensus in the network will be increased, which minimizes conflict. Each pattern being stored in a local minima, we descend to find it. Of course, there is a limited number of patterns that can be stored in this landscape before they start interfering with each other, and that is one of the limitations of the network.
Here is the full notebook:
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
def show_letter(pattern):
# just plots the pattern
f, ax = plt.subplots(1, 1, figsize=(4, 4))
ax.imshow(pattern.reshape(side_len, side_len), cmap='bone_r')
ax.set_axis_off()
f.tight_layout()
def add_noise(x_, noise_level=.2):
noise = np.random.choice(
[1, -1], size=len(x_), p=[1-noise_level, noise_level])
return x_ * noise
# make 2 patterns, the letter A and Z
side_len = 5
A = np.array([
[-1, 1, 1, 1, -1],
[1, -1, - 1, -1, 1],
[1, 1, 1, 1, 1],
[1, -1, - 1, -1, 1],
[1, -1, - 1, -1, 1],
]).reshape(-1)
Z = np.array([
[1, 1, 1, 1, 1],
[-1, -1, -1, 1, -1],
[-1, -1, 1, -1, - 1],
[-1, 1, -1, -1, -1],
[1, 1, 1, 1, 1],
]).reshape(-1)
# show the patterns
show_letter(A)
show_letter(Z)
# creates a 2D NumPy array, X, where each row represents a pattern (e.g., the letters A and Z) that the Hopfield Network will memorize.
X = np.array([A, Z])
X
array([[-1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1,
-1, -1, -1, 1, 1, -1, -1, -1, 1],
[ 1, 1, 1, 1, 1, -1, -1, -1, 1, -1, -1, -1, 1, -1, -1, -1,
1, -1, -1, -1, 1, 1, 1, 1, 1]])
"""
m: The number of patterns to memorize (in this case, 2).
n_units: The number of units (neurons), which corresponds to the length of each
pattern (e.g., the number of pixels if the patterns represent images).
"""
m, n_units = np.shape(X)
m, n_units
(2, 25)
"""
Initializes the weight matrix weights with zeros. This matrix will store the
pairwise connections between neurons in the Hopfield Network.
It is of size n_units × n_units (a fully connected network of neurons).
"""
weights = np.zeros((n_units, n_units))
weights
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0.]])
"""
Implements Hebbian learning to update the weights for storing the patterns in the network.
Iterates over each pattern x in X.
Computes the outer product of the pattern with itself: outer(x,x)=x⋅xT
This captures the interactions between all pairs of neurons for the given pattern.
Divides by m (the number of patterns, 2 in our case) to average the contributions of all patterns to the weights.
Adds the result to the weights matrix.
"""
for x in X: # x is a pattern
weights += np.outer(x, x) / m # outer product with itself. in order to see how each neuron is connected with each neuron.
weights[np.diag_indices(n_units)] = 0 # we want the diagonal to be 0 because the neurons don't have connections between themselves
weights
array([[ 0., 0., 0., 0., 1., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 1., 1., 1., 0.],
[ 0., 0., 1., 1., 0., 0., -1., -1., 0., 0., 0., 0., 1.,
0., 0., 0., 0., -1., -1., 0., 1., 0., 0., 0., 1.],
[ 0., 1., 0., 1., 0., 0., -1., -1., 0., 0., 0., 0., 1.,
0., 0., 0., 0., -1., -1., 0., 1., 0., 0., 0., 1.],
[ 0., 1., 1., 0., 0., 0., -1., -1., 0., 0., 0., 0., 1.,
0., 0., 0., 0., -1., -1., 0., 1., 0., 0., 0., 1.],
[ 1., 0., 0., 0., 0., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 1., 1., 1., 0.],
[-1., 0., 0., 0., -1., 0., 0., 0., -1., 1., 1., 1., 0.,
1., 1., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[ 0., -1., -1., -1., 0., 0., 0., 1., 0., 0., 0., 0., -1.,
0., 0., 0., 0., 1., 1., 0., -1., 0., 0., 0., -1.],
[ 0., -1., -1., -1., 0., 0., 1., 0., 0., 0., 0., 0., -1.,
0., 0., 0., 0., 1., 1., 0., -1., 0., 0., 0., -1.],
[ 1., 0., 0., 0., 1., -1., 0., 0., 0., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 1., 1., 1., 0.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 0., 1., 1., 0.,
1., 1., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 0., 1., 0.,
1., 1., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 1., 0., 0.,
1., 1., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[ 0., 1., 1., 1., 0., 0., -1., -1., 0., 0., 0., 0., 0.,
0., 0., 0., 0., -1., -1., 0., 1., 0., 0., 0., 1.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 1., 1., 0.,
0., 1., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 1., 1., 0.,
1., 0., 1., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 1., 1., 0.,
1., 1., 0., -1., 0., 0., 1., 0., -1., -1., -1., 0.],
[ 1., 0., 0., 0., 1., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 0., 0., 0., -1., 0., 1., 1., 1., 0.],
[ 0., -1., -1., -1., 0., 0., 1., 1., 0., 0., 0., 0., -1.,
0., 0., 0., 0., 0., 1., 0., -1., 0., 0., 0., -1.],
[ 0., -1., -1., -1., 0., 0., 1., 1., 0., 0., 0., 0., -1.,
0., 0., 0., 0., 1., 0., 0., -1., 0., 0., 0., -1.],
[-1., 0., 0., 0., -1., 1., 0., 0., -1., 1., 1., 1., 0.,
1., 1., 1., -1., 0., 0., 0., 0., -1., -1., -1., 0.],
[ 0., 1., 1., 1., 0., 0., -1., -1., 0., 0., 0., 0., 1.,
0., 0., 0., 0., -1., -1., 0., 0., 0., 0., 0., 1.],
[ 1., 0., 0., 0., 1., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 0., 1., 1., 0.],
[ 1., 0., 0., 0., 1., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 1., 0., 1., 0.],
[ 1., 0., 0., 0., 1., -1., 0., 0., 1., -1., -1., -1., 0.,
-1., -1., -1., 1., 0., 0., -1., 0., 1., 1., 0., 0.],
[ 0., 1., 1., 1., 0., 0., -1., -1., 0., 0., 0., 0., 1.,
0., 0., 0., 0., -1., -1., 0., 1., 0., 0., 0., 0.]])
# show the test pattern again
x_test = A
show_letter(x_test)
# add noise
noise_level = .25
x_test = add_noise(x_test, noise_level=noise_level)
show_letter(x_test)
def pattern_complete(weights, X, n_iter=10, soft=False):
Xs = [None] * n_iter # This list will store the state of X after each iteration.
for i in range(n_iter):
X = np.dot(X, weights) # X (the current pattern) is multiplied by the weight matrix (inner product).
if soft:
X = np.tanh(X) # Uses the hyperbolic tangent (tanh) function to smooth updates. Newer Hopfield networks.
else:
"""
Hard Activation: Uses thresholding to update the neuron states:
Neurons with negative inputs are set to −1
Neurons with non-negative inputs are set to +1.
This binary update aligns with the classical Hopfield network.
"""
X[X < 0] = -1
X[X >= 0] = 1
Xs[i] = X # Saves the current state of X in the ith slot of Xs. This allows tracking how X evolves over iterations.
return Xs # The final element of Xs represents the converged state
# pattern completion
n_iter = 2
x_hats = pattern_complete(weights, x_test, n_iter=n_iter)
# show_letter(x_hats[-1])
f, axes = plt.subplots(1, n_iter+1, figsize=((n_iter+1)*3, 3))
x_hats.insert(0, x_test)
for i in range(n_iter+1):
axes[i].imshow(x_hats[i].reshape(side_len, side_len), cmap='bone_r')
axes[i].set_axis_off()
axes[i].set_title(f'pattern completion, iter: {i}')
f.tight_layout()
